Excel: fórmulas matriciais

Fórmulas matriciais são utilizadas para fazer verdadeiros milagres no Excel, conheça um pouco mais deste aspecto pouco conhecido do Excel.

por Robert Martim

Neste artigo, estarei cobrindo um aspecto pouco conhecido do Excel: fórmulas matriciais.

Fórmulas matriciais são utilizadas para fazer verdadeiros milagres no Excel. O que você está prestes a ler faz parte do manual de treinamento produzido para o Linha de Código o qual pode ser adquirido em http://shop.linhadecodigo.com.br/treinamento.asp?id=297

Esta é apenas uma parte do que você encontrará nas 670 páginas deste treinamento. O treinamento é dividido em módulos o que facilitará o sua compreensão e assimilação do conteúdo.

Este tutorial assume que você tem um conhecimento básico de fórmulas matriciais e compreende o processo de edição e entrada de fórmulas matriciais. Se este não for o seu caso, adquira o manual de treinamento onde você encontrará tudo que você precisa saber sobre fórmulas matriciais e muito mais.

Imagine que você possui o seguinte conjuntos de dados:

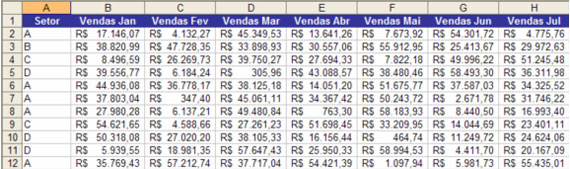
Figura 1: Dados utilizados na solução do problema

O seu chefe solicita um somatório para o setor A para o segundo trimestre (abril, maio e junho). Em outras palavras, a fórmula impossível que o seu chefe quer ver no Excel precisa calcular os intervalos conforme a figura abaixo:

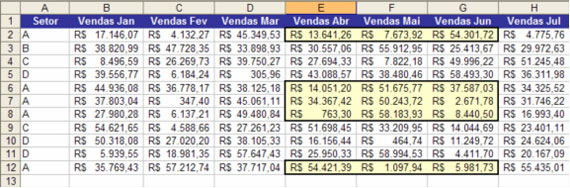
Figura 2: Visualizando o que o problema requer

Você leva as mãos à cabeça, se desespera e chegaa conclusão que isolar este intervalo é impossível. Impossível porque o seu chefe quer ter a flexibilidade de poder somar outros intervalos para outros setores. Ou seja, não basta simplesmente selecionar manualmente as áreas. A sua fórmula precisa ser dinâmica o suficiente para que ao entrar os critérios de soma, a fórmula seja capaz de interpretar os critérios e somar os valores dentro do intervalo total que vai de B2:H12.

Se já era impossível somar antes, com as novas informações você realmente começa a achar que seu chefe está brincando porque fazer isso simplesmente não dá.

Se você realmente acredita na impossobilidade, você desistirá antes mesmo de tentar encontrar uma solução.

A figura anterior mostra o resumo de nosso problema. A fórmula será baseada em dois critérios: Setor e Intervalo de vendas . Aqui, os nossos critérios são o setor A e as vendas entre abril e junho.

Se você nunca utilizou a função DESLOC , o conceito parecerá um pouco estranho no início, mas ao desvendar os mistérios desta função você verá que há muitas outras utilidades para ela.

Primeiramente, vamos construir a tabela de forma que os critérios possam ser inseridos nas células:

Figura 3: Formatando os campos de entrada de critérios

É boa prática não digitar valores diretamente nas fórmulas. Ao alimentar a fórmula a partir de outras células não precisamos mais mexer na fórmula uma vez que ela esteja pronta.

Com a configuração de nossa planilha pronta, podemos iniciar o somatório. Na célula D2, entraremos a fórmula:

{=SOMA((A6:A16=B1)*(DESLOC(B6:H16;0;CORRESP(B2;B5:H5;0)-1;;CORRESP(B3;B5:H5;0)-
CORRESP(B2;B5:H5;0)+1)))}

O que a fórmula faz é o seguinte:

1. Retorna uma matriz contendo verdadeiro e falsos (A6:A16=B1)
2. A função DESLOC retorna uma matriz 11 x 3. Esta matriz é obtida da seguinte forma:
   1. Referência de deslocamento é a área que contém os dados para avaliação;
   2. O deslocamento de linhas é zero e o deslocamento em colunas é dado por N – 1 onde N é encontrado por CORRESP(B2;B5:H5;0) ;
   3. É desnecessário calcular a altura, pois não estamos interessados na altura da matriz;
   4. A largura do deslocamento é a diferença entre a coluna superior ( CORRESP(B3;B5:H5;0) ) menos a coluna inferior ( CORRESP(B2;B5:H5;0) ). Este resultado é somado a 1, pois obteremos uma coluna a menos na subtração.
3. As matriz obtidas em 1 e 2 acima são multiplicadas retornando uma nova matriz contendo zeros e os valores em 2 que são verdadeiros
4. Esta matriz final é; então, somada.

Na pasta de trabalho que acompanha o treinamento, todos os cálculos são desenvolvidos passo-a-passo para uma melhor compreensão.

E se o somatório contivesse mais de um critério? Podemos adaptar a fórmula da seguinte maneira:

{=SOMA(((A6:A16=B1)+(A6:A16=C1))*(DESLOC(B6:H16;0;CORRESP(B2;B5:H5;0)-
1;;CORRESP(B3;B5:H5;0)-CORRESP(B2;B5:H5;0)+1)))}

Aqui, estou avaliando as condições nas células B1 e C1. Cada avaliação retorna uma matriz contendo verdadeiros e falsos. O que você precisa lembrar é que ao multiplicar estas duas matrizes você está avaliando a condição quando AMBOS os critérios são verdadeiros (quando o primeiro e o segundo são verdadeiros – uma avaliação equivalente a função E() ).

Como desejamos saber quando um OU outro é verdadeiro (uma avaliação equivalente a função OU() ), precisamos somar estas duas novas matrizes para obter uma terceira matriz contendo verdadeiros e falsos.

Figura 4: Solução do problema com dois e três critérios de avaliação

Esta é apenas uma demonstração do poderio de fogo das fórmulas matriciais e o que você encontrará no manual de treinamento produzido para o Linha de Código. Se você ainda não possui o seu visite a loja do Linha de Código em em http://shop.linhadecodigo.com.br/treinamento.asp?id=297 e adquira já o manual de treinamento.

Você não somente aprenderá todos os segredos de fórmulas matriciais (soma em diagonal, multiplos critérios, utilização de switches em fórmulas, etc), mas também aprenderá conceitos avançados de programação em VBA (em alguns casos projetos prontos para uso), fórmulas, formatação condicional e muito mais.

Fique de olho nesta coluna para mais dicas sobre o Excel e Office.